Given:
The principal amount = $500
Interest rate = 10% quarterly
Required:
Find the deposing amount after 25 years.
Step-by-step explanation:
The amount formula when the interest is compounded quarterly is given as:

Where r = interest rate
t = time period
n = The number of compounded times
The amount after 25 years is:
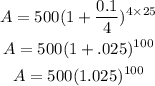
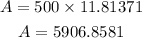
Final Answer:
The amount after 25 years will be &5906.85