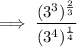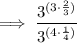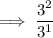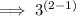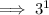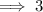Answer:
3
Explanation:
Given expression:
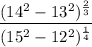
Following the order of operations, carry out the operations inside the parentheses first.
Apply the Difference of Two Square formula
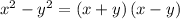
to the operations inside the parentheses in both the numerator and denominator:
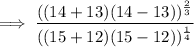
Carry out the operations inside the parentheses:
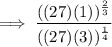

Carry out the prime factorization of 27 and 81.
Therefore, rewrite 27 as 3³ and 81 as 3⁴: