Question

Find the radius of a cylinder whose height is 10 cm and the total surface area is 352 cm².

Answer 1

r ≈ 4 cm

Explanation:

Total Surface Area of a cylinder

A = Base Area x 2 + Lateral Surface Area

A = 2(πr²) + 2πrh

where r = radius of base and h = height of cylinder

Solving for r we get

`\displaystyle r = (1)/(2) \sqrt{h^2 + 2 (A)/(\pi) }-(h)/(2)\\\\`

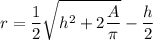
Given h = 10 cm and A = 325 we get

`\displaystyle r = (1)/(2) \sqrt{10^2 + 2 (352)/(\pi) }-(10)/(2)\\\\\\`

`\sqrt{10^2 + 2 (352)/(\pi) } =\sqrt{100+(704)/(\pi )}\\\\= √(100 + 224.09)\\\\\\`

=
`√(324.09)`

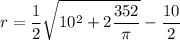
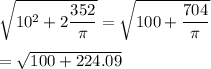
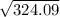
= 18.0025

1/2 x 18.0025 ≈ 9

So r ≈ 9 - 10/2 = 9 -5 = 4

r ≈ 4 cm

Answer 2

Answer: the radius of a cylinder is 4 cm

Explanation:

`S_(ts)=352\ cm\ \ \ \ H=10\ cm\ \ \ \ \ r=?`

The total surface area:

`\displaystyle\\ S_(ts)= 2\pi r^2+2\pi rH\\\\S_(ts)=2\pi (r^2+rH)\\\\352=2\pi (r^2+10r)\\\\`

Divide both parts of the equation by 2π:

`\displaystyle\\56=r^2+10r\\\\56-56=r^2+10r-56\\\\0=r^2+10r-56\\\\Thus,\\\\ r^2+10r-56=0\\\\D=(-10)^2-4(1)(-56)\\\\D=100+224\\\\D=324\\\\√(D)=√(324) \\\\√(D)=18\\\\ r=(-10б18)/(2(1)) \\\\r=-14\\otin\ (r > 0)\\\\r=4\ cm`