Question

NO LINKS!! Please help me with this problem​

Answer 1

`\textsf{c)} \quad 0.3821, \; 0.8745`

Explanation:

Given equation:

`3 \cos (5t)+3=2, \quad \quad 0\leq t\leq (\pi)/(2)`

Rearrange the equation to isolate cos(5t):

`\begin{aligned}\implies 3 \cos(5t)+3&=2\\3 \cos(5t)&=-1\\\cos(5t)&=-(1)/(3)\end{aligned}`

Take the inverse cosine of both sides:

`\implies 5t=\cos^(-1)\left(-(1)/(3)\right)`

`\implies 5t=1.91063..., -1.91063...`

As the cosine graph repeats every 2π radians, add 2πn to the answers:

`\implies 5t=1.91063...+2\pi n, -1.91063...+2 \pi n`

Divide both sides by 5:

`\implies t=0.38212...+(2)/(5)\pi n,\;\; -0.38212...+(2)/(5) \pi n`

The given interval is:

`0\leq t\leq (\pi)/(2)\implies0\leq t\leq 1.57079...`

Therefore, the solutions to the equation in the given interval are:

`\implies t=0.3821, \; 0.8745`

Answer 2

Answer: Choice C)

0.3821, 0.8745

========================================================

Work Shown:

pi/2 = 3.14/2 = 1.57 approximately

The solutions for t must be in the interval 0 ≤ t ≤ 1.57

`3\cos(5t)+3 = 2\\\\3\cos(5t) = 2-3\\\\3\cos(5t) = -1\\\\\cos(5t) = -1/3\\\\5t = \cos^(-1)(-1/3)\\\\5t \approx 1.9106+2\pi n \ \text{ or } \ 5t \approx -1.9106+2\pi n\\\\t \approx (1.9106+2\pi n)/(5) \ \text{ or } \ t \approx (-1.9106+2\pi n)/(5)\\\\`

where n is an integer.

Let

`P = (1.9106+2\pi n)/(5)\\\\Q = (-1.9106+2\pi n)/(5)\\\\`

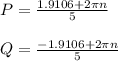
Then let's generate a small table of values like so

`\begin{array}c \cline{1-3}n & P & Q\\\cline{1-3}-1 & -0.8745 & -1.6388\\\cline{1-3}0 & **0.3821** & -0.3821\\\cline{1-3}1 & 1.6388 & **0.8745**\\\cline{1-3}2 & 2.8954 & 2.1312\\\cline{1-3}\end{array}`

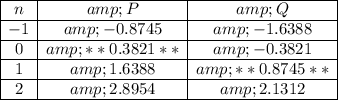
The terms with surrounding double stars represent items in the interval 0 ≤ t ≤ 1.57

Therefore, we end up with the solutions 0.3821 and 0.8745 both of which are approximate.

You can use a graphing tool like Desmos or GeoGebra to verify the solutions. Be sure to restrict the domain to 0 ≤ t ≤ 1.57