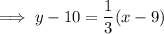Question

HELP PLS A line includes the points (9,10) and (6,9). What is its equation in point-slope form?

Use one of the specified points in your equation. Write your answer using integers, proper fractions, and improper fractions. Simplify all fractions.

Answer 1

`y-10=(1)/(3)(x-9)`

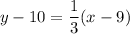
Explanation:

`\boxed{\begin{minipage}{4.4cm}\underline{Slope Formula}\\\\Slope $(m)=(y_2-y_1)/(x_2-x_1)$\\\\where $(x_1,y_1)$ and $(x_2,y_2)$ \\are two points on the line.\\\end{minipage}}`

To find the equation of a line that passes through two given points, first find its slope by substituting the given points into the slope formula.

Define the points:

• (x₁, y₁) = (9, 10)
• (x₂, y₂) = (6, 9)

Substitute the points into the slope formula:

`\implies m=(9-10)/(6-9)=(-1)/(-3)=(1)/(3)`

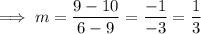
Therefore, the slope of the line is ¹/₃.

`\boxed{\begin{minipage}{5.8 cm}\underline{Point-slope form of a linear equation}\\\\$y-y_1=m(x-x_1)$\\\\where:\\ \phantom{ww}$\bullet$ $m$ is the slope. \\ \phantom{ww}$\bullet$ $(x_1,y_1)$ is a point on the line.\\\end{minipage}}`

To find the equation in point-slope form, simply substitute the found slope and one of the given points into the point-slope formula:

`\implies y-10=(1)/(3)(x-9)`