⇒Logically we know that to find the
 term we use
term we use
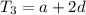
⇒From
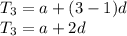
⇒And the
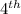 is equal
is equal
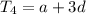 from the same method I used above from the general equation of finding the
from the same method I used above from the general equation of finding the
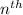 term.
term.
⇒It is said the sum of
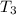 and
and
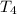 is -2 meaning
is -2 meaning

⇒It is also said that
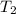 is 2 and we know at this point that
is 2 and we know at this point that
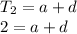
⇒Then we can use the simultaneous equations technique to find the value of d.
I will use the substitution method by deriving the third equation from the second equation 2=a+d
a=2-d is the
 equation that I will substitute in the equation
equation that I will substitute in the equation
In the place of a it means I will plug in 2-d in the place of a.
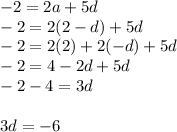
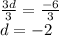
NOTE if you were also asked to find the value of a you can use the equations above to find the value of a which is the first term. the difference represented by letter d is -2.
GOODLUCK!!