Answer:
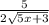
Explanation:
First, use the chain rule to quickly find the answer so that you can check after you go through the ridiculous process that is the bane of every calculus 1 student's existence.
f(x) = (5x + 3)^(1/2)
(d/dx) (5x + 3)^(1/2) =
(1/2)(5x + 3)^(-1/2) * (5) =
5/[2(5x+3)^(1/2)]
Now, we enter the first gate of hell:
f'(x) = the limit as h approaches 0 of [(f(x+h) - f(x))/h]
lim as h -> 0 of [(5(x+h)+3)^(1/2) - (5x+3)^(1/2)/h]
lim as h -> 0 of [(5x+5h+3)^(1/2) - (5x+3)^(1/2) / h]
Multiply numerator and denominator by the conjugate of the numerator, which is (5x+5h+3)^(1/2) + (5x+3)^(1/2).
lim as h -> 0 of
[√(5x+5h+3) - √(5x+3) ] [√(5x+5h+3) + √(5x+3) ]
______________________________________
h[√(5x+5h+3) - √(5x+3) ]
Simplify the numerator via FOIL:
5x+5h+3 + √(5x+5h+3)√(5x+3) - √(5x+3)√(5x+5h+3) - (5x+3)
The remaining radicals in the numerator cancel each-other, giving us:
5x + 5h + 3 - 5x - 3
Simplify Further:
5h
Now that we have simplified our numerator, let's continue:
lim as h -> 0 of (5)(h)/[(h)((5x+5h+3)^(1/2) + (5x+3)^(1/2))]
The h in the numerator cancels the h in the denominator.
lim as h -> 0 of 5/[(5x+5h+3)^(1/2) + (5x+3)^(1/2)]
Now, we directly substitute h with 0 in the equation.
5/[ (5x+3)^1/2 + (5x+3)^(1/2) ]
In the denominator, both sides of the addition sign are the same, so we can simplify it further to:
5/[ 2(5x+3)^(1/2) ]
This is the same answer we received using the chain rule, so it is correct!