Question

Write the equation of a line in slope intercept form that passes through (-15, 20) and is parallel to x - 5y = 5

Answer 1

First step is to write the equation in slope-intercept form

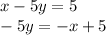`x - 5y = 5\\-5y = -x+5` To make simplification easier, multiply negative to both sides

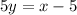`5y = x-5\\` Now, you must divide 5 to both sides to isolate the variable

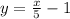`y = (x)/(5) - 1` To tell the slope more easily, turn
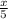`(x)/(5)` into
`(1)/(5) x`

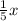
To rewrite the equation:
`y = (1)/(5) x - 1`

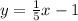
Now, you are able to see the slope(m) being
`(1)/(5)`

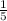
Next, you use the formula y=mx+b to solve for b (replace your newly found slope and points "x" and "y"

`20 = ((1)/(5) *-15) + b\\20 = -3 + b\\b -3 = 20\\b = 23`

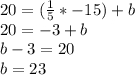
Final Answer:
`y = (1)/(5) + 23`

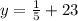
Hope this helps :)