Answer:
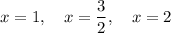
Explanation:
Factor Theorem
If f(x) is a polynomial, and f(a) = 0, then (x – a) is a factor of f(x).
If the coefficients in a polynomial add up to 0, then (x - 1) is a factor.
Given polynomial function:
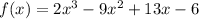
Sum the coefficients:
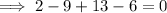
As the sum of the coefficients is zero, (x - 1) is a factor.
Therefore:
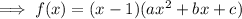
Expand the brackets:
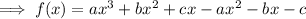
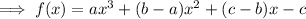
Compare the coefficients with the given polynomial.
As the coefficient of the leading term of the polynomial is 2:
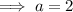
As the coefficient of the term in x² is -9:
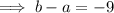
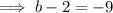
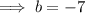
As the constant of the given polynomial is -6:
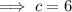
Substitute the found values of a, b and c into the factored form of the polynomial:
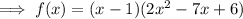
Factor the quadratic:
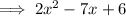
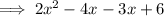
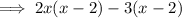
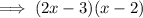
Therefore, the fully factored polynomial is:
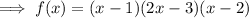
To find the zeros, set the function to zero:
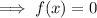
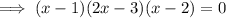
Apply the zero-product property:
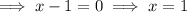
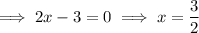
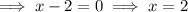
Therefore, the real zeros of the given polynomial are 1, ³/₂ and 2.