Answer:
F = (-22, 4)
Explanation:
Midpoint between two points
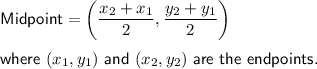
Given information:
- Midpoint = (-6, -2)
- E = (10, -8)
Define the endpoints of the line segment EF:
- Let (x₁, y₁) = endpoint E = (10, -8)
- Let (x₂, y₂) = endpoint F
Substitute the given information into the formula:
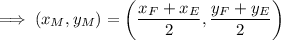
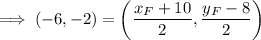
Find the x-coordinate of M:
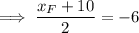
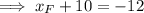
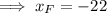
Find the y-coordinate of M:
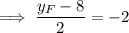

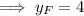
Therefore, the coordinates of endpoint F are (-22, 4).