Answer:
At least
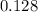 (rounded up, to three significant figures as in speed,) assuming that the road is level and that
(rounded up, to three significant figures as in speed,) assuming that the road is level and that
 .
.
Step-by-step explanation:
When an object is in a circular motion, the magnitude of the net force can be found in terms of the mass and speed of that object, as well as the radius of the circular path:
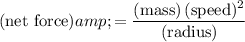 .
.
Let
 denote the mass of this vehicle. Let
denote the mass of this vehicle. Let
 denote the speed of this vehicle. Let
denote the speed of this vehicle. Let
 denote the radius of this circular path. While in this circular motion, the magnitude of the net force will be on this vehicle will be:
denote the radius of this circular path. While in this circular motion, the magnitude of the net force will be on this vehicle will be:
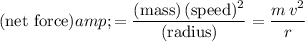 .
.
Forces on this vehicle include:
- Gravitational attraction from the earth (weight) of magnitude
 , pointing downwards,
, pointing downwards, - Normal force from the road, pointing upwards, and
- Static friction from the road, pointing towards the center of the curve.
If this road is level, the normal force from the road will balance the weight of this vehicle. The magnitude of the normal force will be equal to that of the weight of this vehicle,
 .
.
Let
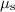 denote the static friction coefficient between the tire and the road. The static friction between the vehicle and the road cannot exceed
denote the static friction coefficient between the tire and the road. The static friction between the vehicle and the road cannot exceed
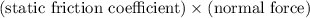 .
.
Since
 , the maximum possible value of static friction will be:
, the maximum possible value of static friction will be:
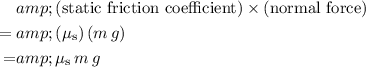 .
.
Under the assumptions, the weight and normal force on this vehicle will be balanced. As a result, the net force on this vehicle will be equal to static friction and should also be no greater than
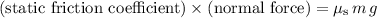 .
.
In other words:
 .
.
Additionally, from circular motion:
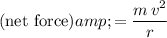 .
.
Therefore:
 .
.
Rearrange this inequality to separate the coefficient of static friction,
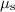 :
:
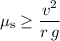 .
.
(Note that
 and
and
 are both greater than
are both greater than
 .)
.)
Substitute in
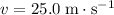 ,
,
 , and
, and
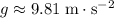 :
:
 .
.
(Rounded up.)