Answer:
1. Choice (2) 13
2. Choice (3) 8.1
3. Choice (3) 95 to 105 ft
4. Choice (3) 96 in
Explanation:
All the problems use the Pythagorean theorem
The Pythagorean Theorem states that the sum of the squared sides of a right triangle equals the length of the hypotenuse squared.
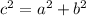
or
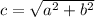
where c is the hypotenuse and a, b the shorter sides.
This means that given any two of the three sides of a right triangle we can compute the length of the third side
For example if we were given the hypotenuse c and side b, we can solve for side a by:
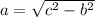
If we were given side a and asked to solve for side b then
b = \sqrt{c^{2} - a^{2}}
Frankly it does not matter which you choose as side a and side b.
Question 1
The distance from the foot of the ladder to the wall can be taken to be side a and is equal to 8ft
So b = 8ft
The length of the ladder is the hypotenuse c = 15 feet

Rounded to nearest foot, that would be 13 feet So choice (2)
Question 2
The points J and K have the following coordinates as indicated on the graph.
J(-3, 2)
K (1, -5)
The distance between two points is the length of the path connecting them. The shortest path distance is a straight line. In a 2 dimensional plane, the distance between points (X1, Y1) and (X2, Y2) is given by the Pythagorean theorem:
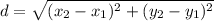
For:
(X1, Y1) = (-3, 2)
(X2, Y2) = (1, -5)
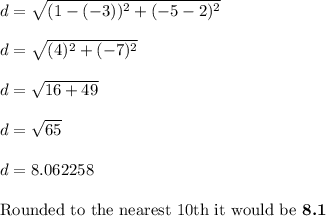 So choice (3)
So choice (3)
Question 3
This again involves a right triangle as shown in the figure
The sides are a = AC = 60 and b = BC = 80 and we are asked to find the length of AC which is the hypotenuse of ΔABC
Use the Pythagorean Theorem directly
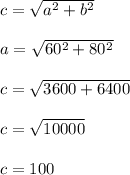
Answer 100 feet so choice (3): from 95 to 105 ft
Question 4
The brace is one of the shorter sides, with the platform top as the hypotenuse.
Let's use a for the brace, b for the 40 in side and c for the hypotenuse = 104 in
So we have to compute for b using the formula:
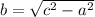
Using the given values, this would be:
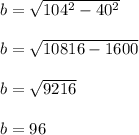
which would be choice (3)