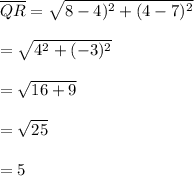Question

Coordinates of a parallelogram are P(0,2) Q(4,7) R(8,4) S(4,-1)

what is the area of the parallelogram?

Answer 1

32 square units

Explanation:

A plot of the points shows that PQRS is a rectangle.

The length of this is the distance of the segment PQ = distance of segment RS = 6.4 units

The width QR = width PS = 5 units

The area is 5 x 6.4 = 32 square units

Lengths are calculated as follows

Finding length of PQ using distance formula:

`\overline{PQ} = √((4-0)^2 + ((7-2)^2)\\\\= √(4^2 + 5^2)\\\\= √(16 + 25)\\\\= √(41)\\\\= 6.4\\`

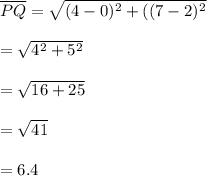
Finding length of QR using distance formula:

`\overline{QR} = √(8-4)^2 + (4 - 7)^2)\\\\= √(4^2 + (-3)^2)\\\\= √(16 + 9)\\\\=√(25)\\\\= 5\\`