Question

What is What is m∠DHG?

Answer 1

Answer: 72 degrees

Step-by-step explanation: We know that angle DHG and angle EHF are congruent due to the vertical angles theorem. Since these two angle measures are congruent, this also means that the expression 6(x-2) is congruent to 3x+30. To find the angle measure of DHG, we need to find x. We can set these two expressions equal to each other and solve for x.

6(x-2) = 3x+30

6x-12 = 3x + 30

-3x -3x

3x-12=30

+12 +12

3x=42

~divide by 3 on both sides~

x = 14

Now that we know our x variable, we can substitute 14 into the expression for angle DHG.

6(14-2)

6(12)

72.

Answer 2

∠DHG = 72°

Explanation:

As ∠DHG and ∠EHF are vertical angles, they are congruent.

What are vertical angles?

Vertical angles are formed when two lines intersect, creating opposite angles. Those opposites are congruent (equal).

Equation:

∠DHG = ∠EHF

[6(x - 2)] = (3x + 30)

Step 1: Distribute 6 through the parentheses.

`\implies 6(x) + 6(-2) = 3x + 30`

`\implies 6x - 12 = 3x + 30`

Step 2: Subtract 3x from both sides.

`\implies 6x - 3x - 12 = 30`

`\implies 3x - 12 = 30`

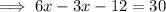
Step 3: Add 12 to both sides.

`\implies 3x - 12 + 12 = 30 + 12`

`\implies 3x = 42`

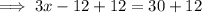
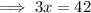
Step 4: Divide both sides by 3.

`\implies (3x)/(3) = (42)/(3)`

`\implies \boxed{x = 14}`

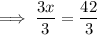
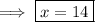
Step 5: Substitute the value of x into ∠DHG to find its measure.

`\implies \angle DHG = 6(14 - 2)`

`\implies \angle DHG = 6(12)`

`\implies \angle DHG = \boxed{72^\circ}`

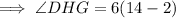
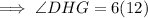
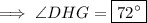
Therefore, the measure of ∠DHG is 72°.