Answer:
y = 2
Explanation:
A horizontal asymptote is a horizontal line that the graph of a function approaches as x approaches ±∞.
Mathematically we write this as
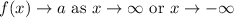
A vertical asymptote at some constant a is where the function approaches ±∞.
Mathematically
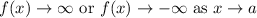
The given function y = 2ˣ + 2 is an exponential function and exponential functions do not have a vertical asymptote
The horizontal asymptote can be found by determining what the function limit is as
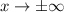
As
 the function
the function
As
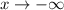 ,
,
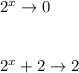
So the equation for the horizontal asymptote is y = 2
The graph shows that at y = 2, the function is parallel to the line but does not touch the line