Question

What is the distance between the points (3,4) and (1,5)?

Answer 1

distance between the points (3,4) and (1,5) = 2.236

Explanation:

The distance between two points is the length of the path connecting them. The shortest path distance is a straight line. In a 2 dimensional plane, the distance between points (X1, Y1) and (X2, Y2) is given by the Pythagorean theorem:

`d = \sqrt {(x_(2) - x_(1))^2 + (y_(2) - y_(1))^2}`'

For:

`(X1, Y1) = (3, 4)\\\\(X2, Y2) = (1, 5)`

`d = \sqrt {(1 - 3)^2 + (5 - 4)^2}\\\\d = \sqrt {(-2)^2 + (1)^2}\\\\d = \sqrt {{4} + {1}}\\\\d = \sqrt {5}\\\\d = 2.236068`

Answer 2

Exact distance is
`√(5)`

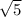
Approximate distance is 2.2361

Round the decimal value however your teacher instructs.

====================================================

Work Shown:

I used the distance formula to get the following.

`(x_1,y_1) = (3,4) \text{ and } (x_2, y_2) = (1,5)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((3-1)^2 + (4-5)^2)\\\\d = √((2)^2 + (-1)^2)\\\\d = √(4 + 1)\\\\d = √(5)\\\\d \approx 2.2361\\\\`

----------------

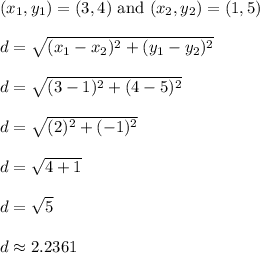
A slight alternative is to plot the points A(3,4) and B(1,5) and C(3,5).

Points A and B are the original points we were given. Point C helps form a right triangle. The hypotenuse is AB and the legs are AC and BC.

Leg AC = 1 unit and leg BC = 2 units

Use the pythagorean theorem
`a^2+b^2 = c^2` to plug in a = 1 and b = 2 to find that the hypotenuse is exactly
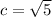`c = √(5)` units long, which is the distance from A to B.