Answer:
Exact distance is
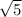
Approximate distance is 2.2361
Round the decimal value however your teacher instructs.
====================================================
Work Shown:
I used the distance formula to get the following.
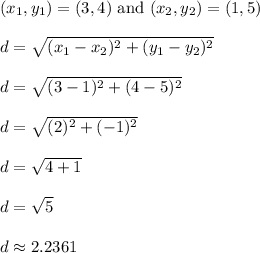
----------------
A slight alternative is to plot the points A(3,4) and B(1,5) and C(3,5).
Points A and B are the original points we were given. Point C helps form a right triangle. The hypotenuse is AB and the legs are AC and BC.
Leg AC = 1 unit and leg BC = 2 units
Use the pythagorean theorem
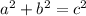 to plug in a = 1 and b = 2 to find that the hypotenuse is exactly
to plug in a = 1 and b = 2 to find that the hypotenuse is exactly
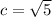 units long, which is the distance from A to B.
units long, which is the distance from A to B.