Question

Find the standard form of the equation of the circle having the following properties:

Center at the origin
Containing the point (-3,8)

Answer 1

Answer: x^2 + y^2 = 73

Explanation:

H, K would be the center

R would be the radius

H, K= 0,0

(x-0)^2 + (y-0)^2= r^2

x^2 + y^2= r ^2

To Find Radius, you find distance between Origin, and Point

`D=\sqrt{(x2-x1)^(2)+(y2-y1)^(2) }`

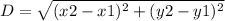
X2, Y2= (-3, 8)

X1, Y1= (0,0)

`D= \sqrt{((-3)-(0))^(2) + ((8-0))^2} \\D= √((-3)^2 + (8)^2) \\D= √(9+ 64) \\D=√(73) \\D= 6√(2)`

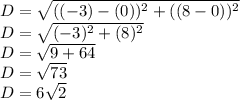
R= 6
`√(2)`

x^2+y^2= (6
`√(2)`)

or x^2+y^2= 73