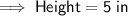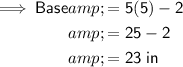Answer:
Height = 5 in
Base = 23 in
Explanation:
Let x be the height of the rectangle.
Given values:
- Height = x in
- Base = (5x - 2) in
- Area = 115 in²
Substitute the values into the formula for area and solve for x:

As length is positive, x = 5.
To find the rectangle's dimensions, substitute the found value of x into the expressions for the height and base: