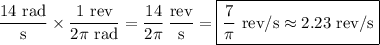Question

A pulley is turning at an angular velocity of 14.0 rad per second. How many revolutions is the pulley making each second? (Hint: one revolution equals 2 pi rad)

Answer 1

7/π ≈ 2.23 revolutions per second

Explanation:

You want the know the angular velocity in revolutions per second of a pulley turning at 14.0 radians per second.

Unit Conversion

The velocity in rad/s can be converted to rev/s using the conversion factor ...

1 rev = 2π rad

The angular velocity is ...

`\frac{14\text{ rad}}{\text{s}}*\frac{1\text{ rev}}{2\pi\text{ rad}}=(14)/(2\pi)\,\frac{\text{rev}}{\text{s}}=\boxed{(7)/(\pi)\text{ rev/s}\approx2.23\text{ rev/s}}`