Question

A bag contains 6 red marbles and 4 yellow marbles. A marble is drawn at random and not replaced. Two further draws are made, again without replacement.

What is the probability of drawing at least one red marble?

Answer 1

6/10

Explanation:

I think, however I may be very wrong, sorry.

Answer 2

`\sf (29)/(30)`

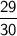
Explanation:

A bag contains:

• 6 red marbles.
• 4 yellow marbles.

Therefore, the total number of marbles in the bag is 10 marbles.

The possible outcomes for drawing 3 marbles (without replacement) are:

• R R R
• R R Y
• R Y R
• R Y Y
• Y R R
• Y R Y
• Y Y R
• Y Y Y

Therefore, the only outcome where at least one red marble is not drawn is {Y Y Y}.

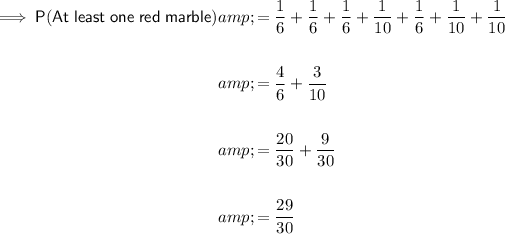
To find the probability of drawing at least one red marble, subtract the probability of drawing 3 yellow marbles from one.

The probability of drawing 3 yellow marbles without replacement is:

`\implies\sf P(3\; yellow \;marbles)=(4)/(10) * (3)/(9) * (2)/(8)=(24)/(720)=(1)/(30)`

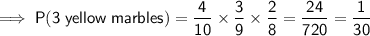
Therefore, the probability of drawing at least one red marble is:

`\implies \sf P(At\;least\;one\;red\;marble)=1-(1)/(30)=(29)/(30)`

This can be confirmed by drawing a tree diagram (see attached).

To find the probability of drawing at least one red marble, add the probabilities at the end of each relevant final branch:

`\begin{aligned}\implies \sf P(At\;least\;one\;red\;marble)&=(1)/(6)+(1)/(6)+(1)/(6)+(1)/(10)+(1)/(6)+(1)/(10)+(1)/(10)\\\\&=(4)/(6)+(3)/(10)\\\\&=(20)/(30)+(9)/(30)\\\\&=(29)/(30)\end{aligned}`