Answer:
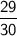
Explanation:
A bag contains:
- 6 red marbles.
- 4 yellow marbles.
Therefore, the total number of marbles in the bag is 10 marbles.
The possible outcomes for drawing 3 marbles (without replacement) are:
- R R R
- R R Y
- R Y R
- R Y Y
- Y R R
- Y R Y
- Y Y R
- Y Y Y
Therefore, the only outcome where at least one red marble is not drawn is {Y Y Y}.
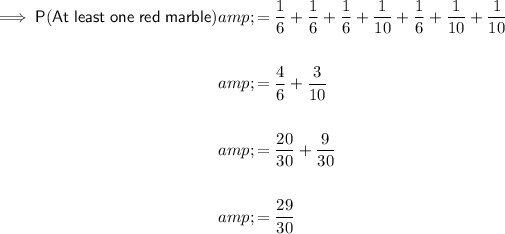
To find the probability of drawing at least one red marble, subtract the probability of drawing 3 yellow marbles from one.
The probability of drawing 3 yellow marbles without replacement is:
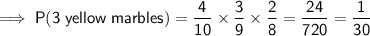
Therefore, the probability of drawing at least one red marble is:

This can be confirmed by drawing a tree diagram (see attached).
To find the probability of drawing at least one red marble, add the probabilities at the end of each relevant final branch: