The correct answer is: [D]: "
 ".
".
______
Explanation:
We are given:
" 5x + 2y = -10 " ; Find the slope of the equation.
______
Rewrite this equation in slope-intercept format ;
that is: " y = mx + b " ;
in which:
y remains as single value, as an 'output' ; or 'dependent
variable', on the 'y-axis' (if graphed);
isolated on the 'left-hand side' of the equation.
m is the coefficient of x in the equation; and represents the slope; for which we shall solve.
{If there is no slope, then "m = 0" ; and "[0 * x = 0]." };
And the "slope-intercept format" is: "y = b" }.
b represents the "y-intercept" ; i.e. when the line crosses the
"y-axis" when graphed; that is, the "y-value" of the "coordinate" of the "y-intercept" ; [i.e. the value of "y" when "x = 0" ; so; " (0, b) ".
{ Note: b can equal "0" ; in those cases: y = mx + 0 ; write as " y = mx "}.
{ If there is no slope, [i.e. "m = 0" ; and no "y-intercept" ; [i.e. "b = 0"];
Then: write the equation accordingly—e.g. " y = [whatever number the graph represents]." }.
Also, note that b can be a "negative number"; as well.
In that case, write an equation in "slope-intercept format" ; that is;
→" y = mx + b " ; as: " y = mx " .
______
Given: " 5x + 2y = -10 " ;
Let's rewrite: ↔ " 2y + 5x = -10 " ; to get the "y-value" a bit closer to the 'left-hand side' of the equation.
Then: Let's subtract 5x from Each Side of the equation;
2y + 5x − 5x = -10 − 5x ;
to get: " 2y = -10 − 5x " ;
______
Method 1):
We have: " 2y = -10 − 5x " ;
Divide Each Side by 2 ; to isolate y on the 'left-hand side' of the equation, and to rewrite as an equation in the slope-intercept format :
2y / 2 = (-10 − 5x)/2 ;
→
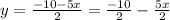 ;
;
→
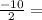 -10 ÷ 2 = -5 ;
-10 ÷ 2 = -5 ;
Rewrite the equation by replacing "
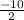 " ; with: -5 ;
" ; with: -5 ;
→
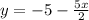 ;
;
Then, rewrite to get the equation in "slope-intercept format"
→
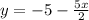 ;
;
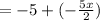 ; ↔ Rewrite:
; ↔ Rewrite:
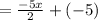 ; ↔ Rewrite again:
; ↔ Rewrite again:
 ;
;
→
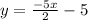 .
.
Note: "
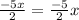 " ;
" ;
→
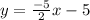 ;
;
This is the equation written in "slope-intercept format" ;
that is: " y = mx + b " ;
in which:
y is isolated as a single variable on the 'left-hand side' of the equation;
m =
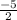 ; which is the slope; which is also the "coefficient" of x ;
; which is the slope; which is also the "coefficient" of x ;
b = -5 ; which is the 'y-coordinate' of the "y-intercept" of the graph;
So, the slope; "m = -5/2" ; is the correct answer; which corresponds to:
Answer choice: [D]: " m =
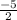 " .
" .
______
Method 2):
Given: " 5x + 2y = -10" ; Find the slope of the line.
We want to rewrite the equation in the "slope-intercept format" ;
" y = mx + b " ; as explained above;
to get the correct answer for m, the slope of the line.
" 5x + 2y = -10 " ↔ Rewrite as:
2y + 5x = -10 ; since we want to isolate y as a single variable on the 'left-hand side' of the equation; and by rearranging & rewriting this equation, the 2y is closer to the 'left' of the equation.
Now, subtract 5x from Each Side of the equation:
2y + 5x − 5x = -10 − 5x ;
to get: 2y = -10 − 5x ;
Now, Let's multiply the entire equation (i.e. "Each Side") by -1 ;
to make the equation easier to handle;
-1(2y) = -1 (-10 − 5x) ;
For the 'left-hand side' of the equation:
-1*2y = -2y
For the 'right-hand side' of the equation:
Note the 'distributive property of multiplication'; as follows:
a(b + c) = ab + ac ;
Likewise:
-1(-10 − 5x) = (-1 *-10) + (-1 *-5x) ;
= (10) + (5x) = 10 + 5x ;
Now, rewrite the entire equation:
-2y = 10 + 5x ; ↔ Rewrite as;
-2y = 5x + 10 ;
Then, we divide Each Side of the equation by -2 ;
to isolate y as a "single variable" on the 'left-hand side' of the equation;
and to rewrite the equation in "slope-intercept format" ;
-2y / -2 = (5x + 10) /-2 ;
→
 ;
;
→
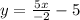 ;
;
which is written in "slope-intercept format" ; that is:
" y = mx + b " ;
in which:
y is isolated as a single variable on the 'left-hand side' of the equation;
m =
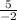 ; which does equal "
; which does equal "
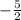 " ; which does equal "
" ; which does equal "
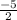 " ;
" ;
which is the slope of the equation, as well as the 'coefficent of x' ;
b = -5 ; which is the 'y-coordinate' of the "y-intercept".
______
As such:
The correct answer choice is: [D]: " m =
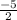 " .
" .
{Note: This is consistent with the answer choice from Method 1 above.}
______
Hope this answer and explanation is helpful.
Best of luck to you!
______