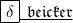Answer:
Answer: y = -x - 1
Explanation:
- Consider a straight line passing through (x, y) from the origin (0, 0). That line with a positive gradient of m and meets at a point (0, c) [y-intercept]
- It has a general equation as below;

- So, consider the line given in our question; Let's find its slope m first;

- From the points given in the question, (-7, 6) and (3, -4)
- x_1 is -7
- x_2 is 3
- y_1 is 6
- y_2 is -4
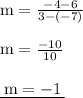
- Therefore, our equation so far is y = -x + c. Our line has a negative slope that means it slants from top to bottom, its origin is its y-intercept
- Consider point (3, -4);
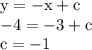
- y-intercept is -1
hence equation is y = -x - 1