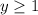Answer:
8a)
D:
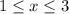 .
.
R:
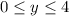
8b)
D:
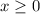
R:
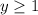
Explanation:
8a) The domain is the set of all possible numbers the x values could be. If there is no corresponding y value for an x value, that x value would not be considered part of the domain.
In the question, the function starts at x = 1 and continues until 3. The ends of the function are closed, so it is inclusive. This can be written as
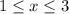 .
.
The range is all the possible y values. The function does not go below y = 0 and has a maximum of 4. The ends of the function are closed, so it is inclusive. This can be written as
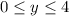
8b) We can do the same for this problem. The x has a minimum at 0 and continues to go on without an upper bound(as indicated by the arrow), is also includes the point where x=0. Therefore, the domain can be written as
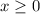 .
.
As for the range, the y minimum is 1 and the function continues to increase as shown by the upwards slope and arrow. The function also includes the point where y=1, so it can written as