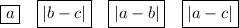Question

Order the following expressions from least to greatest.

Answer 1

`\boxed{a} \quad \boxed \quad \boxeda - b \quad \boxed`

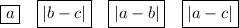
Explanation:

The bars either side of an expression or a value are the absolute value symbol. "Absolute value" means how far a number is from zero. Therefore, the absolute value of a number is its positive numerical value.

The values of a, b and c are negative. All expressions except "a" are absolute values, and are therefore positive numerical values. Therefore, "a" is the least expression.

The simplest way to calculate each expression's numerical value is by assigning approximate numbers to each value, then carrying out each calculation.

From inspection of the graph:

• a ≈ -3.8
• b ≈ -1.3
• c ≈ -0.7

`\begin{aligned} \implies |a - b| & \approx |-3.8 - (-1.3)|\\ & = |-2.5| \\ &= 2.5\end{aligned}`

`\begin{aligned} \implies |b - c| &\approx |-1.3 - (-0.7)| \\ &= |-0.6| \\ &= 0.6\end{aligned}`

`\implies a \approx -3.8`

`\begin{aligned} \implies |a - c| &\approx |-3.8 - (-0.7)| \\ &= |-3.1| \\ &= 3.1\end{aligned}`

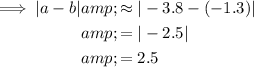
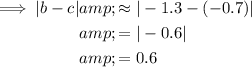
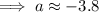
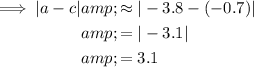
Therefore: -3.8 < 0.6 < 2.5 < 3.1

Hence, the expressions from least to greatest are:

`\boxed{a} \quad \boxedb - c \quad \boxeda - b \quad \boxed`