Question

Graph the solution to this inequality on the number line.

−12≥−4p

Answer 1

The solution to the inequality
`\(-12 \geq -4p\)` can be represented textually as:

`\[ p \geq 3 \]`

This means that the set of values for p satisfying the inequality includes all real numbers greater than or equal to 3.

To graph the solution to the inequality
`\(-12 \geq -4p\)`, we can start by isolating p.

Divide both sides of the inequality by -4, remembering to reverse the inequality sign when dividing by a negative number:

`\[ -12 \geq -4p \]\[ (-12)/(-4) \leq p \]\[ 3 \leq p \]`

Now, we represent this on a number line:

1. Mark a point at 3 on the number line.

2. Draw a solid dot at 3 to include 3 in the solution set because of the inequality sign
`\(\leq\)`.

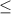3. Extend the line to the right, indicating that p can be any value greater than or equal to 3.

The graph on the number line shows that the solution set for p includes all real numbers greater than or equal to 3.

Answer 2

A closed circle on 3 going right.

Explanation:

-12 ≥ -4p

/-4 /-4

3 ≤ p which also mean p ≥ 3

This will be a closed circle on 3 going right.

Hope that helps!