Question

Help PLEASE!!! How do I solve this?

Answer 1

Two similar boxes A and B are given with box B created by dividing box A's dimensions by 2.

Recall that the scale factor, k is the ratio of lengths of two corresponding sides of similar figures.

Since the dimensions of A were divided by 2 to form B, it follows that the scale factor of box A to box B is:

`k=(2)/(1)`

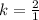
Also, recall the Similar Solids Theorem

It follows that the ratio of the volumes of the given solids is:

`\frac{\text{Volume of A}}{\text{Volume of B }}=k^3=((2)/(1))^3=(2^3)/(1^3)=(8)/(1)`

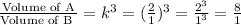
Let the volume of box A be V₁ and let the volume of box B be V₂, it, therefore, implies that:

`(V_1)/(V_2)=(8)/(1)`

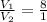
Substitute the value for the volume of box A into the equation, V₁=64:

`\begin{gathered} (64)/(V_2)=(8)/(1) \\ Cross-Multiply_{} \\ \Rightarrow8V_2=64 \\ Divide\text{ both sides by 8:} \\ \Rightarrow(8V_2)/(8)=(64)/(8)\Rightarrow V_2=8\text{ cubic meters} \end{gathered}`

Hence, the volume of box B is 8 m³.