If angle theta is given as;
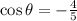
And angle theta is in the third quadrant, then we can find the value of y by using the pythagoras' theorem as follows;

Note also that;
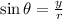
However, the angle theta is in the third quadrant where y is also negative. Therefore, sin theta would be;
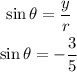
Note also that cosec theta is given as;
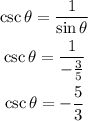
Note also that, tan theta is given as;
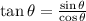
Therefore, we would have;
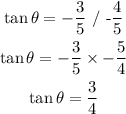
ANSWER:
![undefined]()