SNSWER
. x = 2
F. x = -1
Step-by-step explanation
e can rewrite this equation as a quadratic frunction equal to zero.
First apply the binomial squared on the left side:
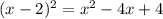
This is to write it in standard form. Now we have the equation:
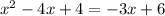
We can add 3x on both sides of the equation:
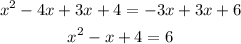
And subtract 6 from both sides:
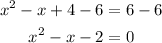
Now we can use the quadratic formula to solve this for x:
![\begin{gathered} ax^2+bx+c=0 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/uuterq6bz1kwr2mb9jy58c523r5v4v644y.png)
In our equation a = 1, b = -1 and c = -2:
![\begin{gathered} x=\frac{1\pm\sqrt[]{1^2+4\cdot2\cdot1}}{2\cdot1} \\ x=\frac{1\pm\sqrt[]{1+8}}{2} \\ x=\frac{1\pm\sqrt[]{9}}{2} \\ x=(1\pm3)/(2) \\ x_1=(1+3)/(2)=(4)/(2)=2_{} \\ x_2=(1-3)/(2)=(-2)/(2)=-1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/5zrqdzq6eap9soioehxjjy97uee8v3zaxm.png)
Therefore the solutions to the given equation are x = 2 and x = -1