Question

What are the solutions of equation (x-2)^2=-3x+6Select all that apply(The choices are in the image)

Answer 1

SNSWER

. x = 2

F. x = -1

Step-by-step explanation

e can rewrite this equation as a quadratic frunction equal to zero.

First apply the binomial squared on the left side:

`(x-2)^2=x^2-4x+4`

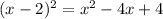
This is to write it in standard form. Now we have the equation:

`x^2-4x+4=-3x+6`

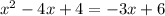
We can add 3x on both sides of the equation:

`\begin{gathered} x^2-4x+3x+4=-3x+3x+6 \\ x^2-x+4=6 \end{gathered}`

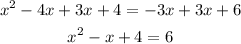
And subtract 6 from both sides:

`\begin{gathered} x^2-x+4-6=6-6 \\ x^2-x-2=0 \end{gathered}`

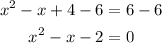
Now we can use the quadratic formula to solve this for x:

`\begin{gathered} ax^2+bx+c=0 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}`

In our equation a = 1, b = -1 and c = -2:

`\begin{gathered} x=\frac{1\pm\sqrt[]{1^2+4\cdot2\cdot1}}{2\cdot1} \\ x=\frac{1\pm\sqrt[]{1+8}}{2} \\ x=\frac{1\pm\sqrt[]{9}}{2} \\ x=(1\pm3)/(2) \\ x_1=(1+3)/(2)=(4)/(2)=2_{} \\ x_2=(1-3)/(2)=(-2)/(2)=-1 \end{gathered}`

Therefore the solutions to the given equation are x = 2 and x = -1