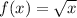 Step-by-step explanation
Step-by-step explanationThe graph of a function f is the set of all points in the plane of the form (x, f(x)).
Step 1
iven
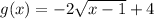
g(x) is a transformation of the function f(x)we have a root in the function, note that the variable x is inside the root, so we can conclude the basic function is
square tooroot
Step 2
rove
ow, lets's check the transformation of f(x)
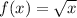
a)1 was subtracted form the argument of the fucnction
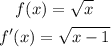
when you subtract a number b form the argument of the function you are shifting the function b units to the rigth
so
he function was shifteed 1 unit to rigth
) the resulting function was multiplied by 2-
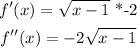
when you multplie by a negavitve constant you are reflecting the funciton acrros x-axis, and is is stretched vertically.
so
he funcition was reflected across x-axis an strtched vertically by a factor of 2
c) 4 was added to the function
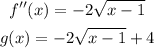
when you add a constant b to any function, the graph will be shifted b units up,so
he functinon was shifted 4 units up
hrerefore, we can conclude the answer is
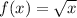
I hope this helps you