We have that the following two points lie on the line:
• (-2, 0) and (4, 6)
And we need to find the equation of the line that passes through both points.
To find the equation of the line, we can proceed as follows:
1. Apply the two-point equation of the line, which is given by:
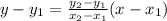
2. We have to label both points as follows:
• (-2, 0) ---> x1 = -2, y1 = 0
• (4, 6) ---> x2 = 4, y2 = 6
3. Now, we can substitute the corresponding points into the two-point equation of the line:
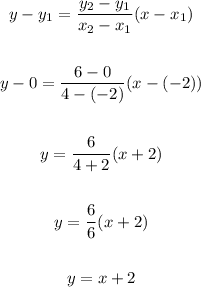
Therefore, we have that the slope of the line is m = 1, and the equation of the line is y = x + 2.
Therefore, in summary, the equation of the line is y = x + 2 (Option D).