Given the equation of an ellipse: #41

To find the center and the vertices, we will complete the square of (x) and (y):
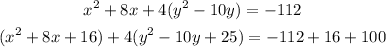
Factor for (x) and (y) then simplify:
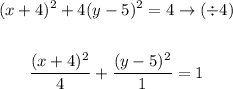
The general form of the ellipse will be:
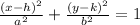
Comparing the equation with the form:
![\begin{gathered} (h,k)=(-4,5) \\ a=\sqrt[]{4}=2 \\ b=\sqrt[]{1}=1 \\ c=\pm\sqrt[]{a^2-b^2}=\pm\sqrt[]{4-1}=\pm\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/aplrk51mblm3qv0s4w7gh0508hsppc3to4.png)
The graph of the ellipse will be as shown in the following picture:
As shown in the figure:
The center C = (h,k) = (-4 , 5)
The vertices denoted by V = (-6, 5) and (-2, 5)
Foci denoted by F =
![(-4+\sqrt[]{3},5),(-4-\sqrt[]{3},5)](https://img.qammunity.org/2023/formulas/mathematics/college/qi6mbojnpw7efmjzwo5kq59h9vk6lpfu9e.png)