Question

For the following exercise graph the given ellipse, noting center, vertices, and foci #41

Answer 1

Given the equation of an ellipse: #41

`x^2+8x+4y^2-40y+112=0`

To find the center and the vertices, we will complete the square of (x) and (y):

`\begin{gathered} x^2+8x+4(y^2-10y)=-112 \\ (x^2+8x+16)+4(y^2-10y+25)=-112+16+100 \end{gathered}`

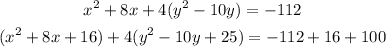
Factor for (x) and (y) then simplify:

`\begin{gathered} (x+4)^2+4(y-5)^2=4\rightarrow(/4) \\ \\ ((x+4)^2)/(4)+((y-5)^2)/(1)=1 \end{gathered}`

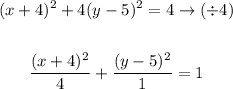
The general form of the ellipse will be:

`((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1`

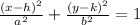
Comparing the equation with the form:

`\begin{gathered} (h,k)=(-4,5) \\ a=\sqrt[]{4}=2 \\ b=\sqrt[]{1}=1 \\ c=\pm\sqrt[]{a^2-b^2}=\pm\sqrt[]{4-1}=\pm\sqrt[]{3} \end{gathered}`

The graph of the ellipse will be as shown in the following picture:

As shown in the figure:

The center C = (h,k) = (-4 , 5)

The vertices denoted by V = (-6, 5) and (-2, 5)

Foci denoted by F =

`(-4+\sqrt[]{3},5),(-4-\sqrt[]{3},5)`