Question

What is the range of the function f(x) = |x – 5| – 3?

R: f(x) ∈ ℝ
R: f(x) < 2
R: f(x) ∈ ℝ
R: f(x) ∈ ℝ

Answer 1

R: f(x) ≥ –3

Explanation:

I got it right on the test.

Answer 2

Answer: Choice C

Reason:

The smallest |x-5| can get is 0 since the result of an absolute value is never negative (because it represents distance).

So the smallest f(x) = |x-5|-3 can get is 0-3 = -3

f(x) = -3 or f(x) > -3 are the only two options for the output f(x).

Condense that into
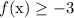`f(\text{x}) \ge -3` to arrive at choice C as the final answer.

The fancy notation of f(x) ∈ ℝ translates to "f(x) is a real number".

If you were to graph this using a tool like Desmos, then notice how the lowest point occurs when y = -3

See the diagram below.