Question

Which ordered pair could you remove from the relation {(–1, 0), (1, 3), (2, 2), (2, 3), (3, 1)} so that it becomes a function

Answer 1

(2,3)

or (2,2) if the function does not need to be continuous.

Explanation:

For a set of points to be considered a function, it must be true that for every X value, you have only a single Y value solution.

In other words, looking through your points listed, you would remove any point where an X value appears twice with different Y values.

`(X,Y)\\(-1,0)\\(1,3)\\(2,2) < -\\(2,3) < -\\(3,1)\\\\`

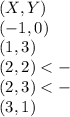
Notice the two points with arrows, both have 2 as their X value, but different Y values. Removing either one of them would make this a function. Although, by removing (2,3) the function has the potential to also be continuous, because having two of the same Y value for different X values would cause a piece-wise function which is generally non-continuous.

Answer 2

Answer:(3,1)

Explanation:

Because you cant have (1,3) and (3,1).