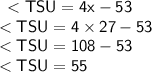Answer:
<TSU = 55°
Explanation:
We know that,
Angle at the circumference of a circle is twice the angle at the centre.
Therefore,
2 × <UST = <UVT
Given that,
< UVT = x + 83
< TSU = 4x - 53
Accordingly, we can make an expression like this.
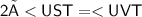
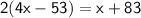
And now solve the above expression and find the value of x.
Let us solve it now.
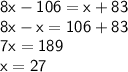
And now, according to the question they've asked us to find the value of <TSU.
As we mentioned earlier, they've given that, <TSU = 4x - 53.
So, to find the value of Angle TSU, we have to replace x with 27 and find the value of angle TSU.
Let us solve it now