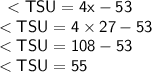Question

How do you solve this

Answer 1

45

Explanation:

In this picture we can see that they gave us 2 angles.

Angle V has an angle of x+83

Angle S has an angle of 4x - 53

As one of the circle thermoses in mathematics said when there is an angle in the center of the circle, the angle at the circumference is half the angle at the center, which means we could create and equation such that:

angle of angle V = 2 times the angle of angle S

x + 83 = 2(4x - 53)

x + 83 = 8x - 106

189 = 7x

27 = x

Since we know x = 27, we can substitute into the equation angle of S to find what is the angle of TSU:

4x - 53

= 4(27) - 53

= 108 - 53

= 45

Answer 2

<TSU = 55°

Explanation:

We know that,

Angle at the circumference of a circle is twice the angle at the centre.

Therefore,

2 × <UST = <UVT

Given that,

< UVT = x + 83

< TSU = 4x - 53

Accordingly, we can make an expression like this.

`\sf2 × <UST = <UVT`

`\sf2(4x - 53) = x + 83 \\`

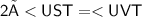
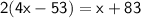
And now solve the above expression and find the value of x.

Let us solve it now.

`\sf8x - 106 = x + 83 \\ \sf8x - x = 106 + 83 \\ \sf7x = 189 \\ \sf \: x = 27`

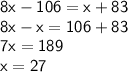
And now, according to the question they've asked us to find the value of <TSU.

As we mentioned earlier, they've given that, <TSU = 4x - 53.

So, to find the value of Angle TSU, we have to replace x with 27 and find the value of angle TSU.

Let us solve it now

`\sf \: <TSU = 4x - 53 \\ \sf \: <TSU = 4 * 27 - 53 \\ \sf \: <TSU = 108 - 53 \\ \sf \: <TSU = 55 \degree`