Give the equation of the circle centered at the origin and passing through the point (4, 0).

Question

asked Jun 9, 2023 42.9k views

1 Answer

Neet · Answer 1 · 2023-06-13T01:15:48+0000

$\quad \huge \quad \quad \boxed{ \tt \:Answer }$

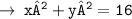
$\qquad \tt \rightarrow \: x² + y² = 16$

____________________________________

$\large \tt Solution \: :$

The distance between the centre and the point through which the circle is passing is equal to the radius of the circle.

so, let's use distance formula here :

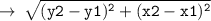
$\qquad \tt \rightarrow \: \sqrt{(y2 - y1) {}^(2) + (x2 - x1) {}^(2) }$

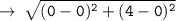
$\qquad \tt \rightarrow \: \sqrt{(0 - 0) {}^(2) + (4 - 0) {}^(2) }$

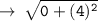
$\qquad \tt \rightarrow \: \sqrt{0 + (4) {}^(2) }$

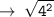
$\qquad \tt \rightarrow \: \sqrt{ {4}^(2) }$

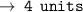
$\qquad \tt \rightarrow \: 4 \: \: units$

Now, let's write the equation of circle in standard form :

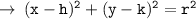
$\qquad \tt \rightarrow \: (x - h) {}^(2) + (y - k) {}^(2) = r {}^(2)$

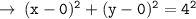
$\qquad \tt \rightarrow \: (x - 0) {}^(2) + (y - 0) {}^(2) = {4}^(2)$

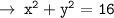
$\qquad \tt \rightarrow \: {x}^(2) + {y}^(2) = 16$

Answered by : ❝ AǫᴜᴀWɪᴢ ❞