Question

Give the equation of the circle centered at the origin and passing through the point (4, 0).

Answer 1

`\quad \huge \quad \quad \boxed{ \tt \:Answer }`

`\qquad \tt \rightarrow \: x² + y² = 16`

____________________________________

`\large \tt Solution \: :`

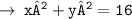
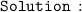
The distance between the centre and the point through which the circle is passing is equal to the radius of the circle.

so, let's use distance formula here :

`\qquad \tt \rightarrow \: \sqrt{(y2 - y1) {}^(2) + (x2 - x1) {}^(2) }`

`\qquad \tt \rightarrow \: \sqrt{(0 - 0) {}^(2) + (4 - 0) {}^(2) }`

`\qquad \tt \rightarrow \: \sqrt{0 + (4) {}^(2) }`

`\qquad \tt \rightarrow \: \sqrt{ {4}^(2) }`

`\qquad \tt \rightarrow \: 4 \: \: units`

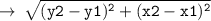
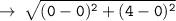
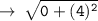
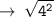
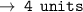
Now, let's write the equation of circle in standard form :

`\qquad \tt \rightarrow \: (x - h) {}^(2) + (y - k) {}^(2) = r {}^(2)`

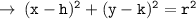
• h = x - coordinate of circle
• k = y - coordinate of circle
• r = radius of circle

`\qquad \tt \rightarrow \: (x - 0) {}^(2) + (y - 0) {}^(2) = {4}^(2)`

`\qquad \tt \rightarrow \: {x}^(2) + {y}^(2) = 16`

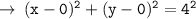
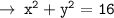
Answered by : ❝ AǫᴜᴀWɪᴢ ❞