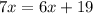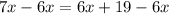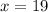Answer:
x= 19
Explanation:
Recall the Vertical Angles Theorem which states that when two lines intersect, vertical angles are congruent. In this case, 7x-8 and 6x +11 are vertical angles, so they are congruent. We can conclude that an equation can be made to find the value of x where:

Solve out the equation to find the value of x.