
We have given in the question that,
- The sum of 2 numbers is equal to 11
- The difference between two numbers is 19 .

- We have to find the value of x and y.
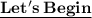
Let the two numbers be x and y
According to the question,


Solving eq( 1 ) we get :-

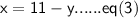
Subsituting eq(3 ) in eq(2) :-
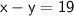
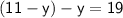

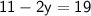
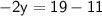
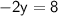
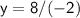
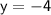

Now, Subsitute the value of y in eq( 3 ) :-
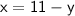
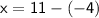
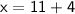
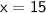
Hence, The value of x and y are 15 and (-4) .