Question

You are standing at the edge of a cliff which is 40 m tall. You throw an apple up with a speed of 15 m/s, and it accelerates downward at 9.81 m/s^2. How long does it take to fall to the bottom of the cliff

Answer 1

Approximately
`4.77\; {\rm s}`.

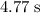Step-by-step explanation:

Let
`u` denote the initial velocity of this apple. Let
`v` denote the velocity of the apple right before landing (final velocity.) Let
`x` denote the displacement of this apple (from the edge to the bottom.) Let
`a` denote the acceleration of this apple. Let
`t` denote the time it takes for the apple to land.

The acceleration of this apple is
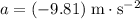`a = (-9.81)\; {\rm m\cdot s^(-2)}`. This value is negative since the apple is accelerating downwards.

It is given that the initial velocity of the apple was
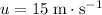`u = 15\; {\rm m\cdot s^(-1)}`. Note that unlike
`a`, the value of
`u` is positive since the apple was initially travelling upwards.

The displacement of the apple would be
`x = (-40)\; {\rm m}`- equal to the height of the cliff in magnitude, but negative since the apple would land at a location below the edge.

Since the acceleration of this apple is a constant value, the SUVAT equation
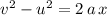`v^(2) - u^(2) = 2\, a\, x` will apply.

Rearrange this equation and solve for
`v` (velocity of apple right before landing):

`\begin{aligned}v^(2) &= 2\, a\, x + u^(2)\end{aligned}`.

Note that the apple will be travelling downward right before it lands. Therefore, the value of
`v` (velocity right before the apple lands) will be negative:

`\begin{aligned}v &= -\sqrt{2\, a\, x + u^(2)}\end{aligned}`.

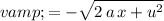Substitute in
`a = (-9.81)\; {\rm m\cdot s^(-2)}`,
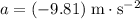`x = (-40)\; {\rm m}`, and
`u = 15\; {\rm m\cdot s^(-1)}`:

`\begin{aligned}v &= -\sqrt{2\, a\, x + u^(2)} \\ &= -\sqrt{2* (-9.81)\; {\rm m\cdot s^(-2)}* (-40)\; {\rm m} + (15\; {\rm m\cdot s^(-1)})^(2)} \\ &\approx -31.78\; {\rm m\cdot s^(-1)}\end{aligned}`.

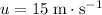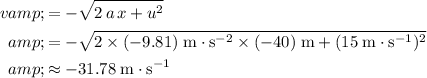In other words, the velocity of the apple would have changed from
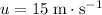`u = 15\; {\rm m\cdot s^(-1)}` to
`(-31.78)\; {\rm m\cdot s^(-1)}` during the flight. The velocity change would be:

`\begin{aligned} \Delta v &= v - u \\ &\approx (-31.78)\; {\rm m\cdot s^(-1)} - 15\; {\rm m\cdot s^(-1)} \\ &= -46.78\; {\rm m\cdot s^(-1)}\end{aligned}`.

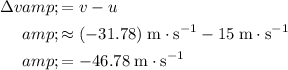At a rate of
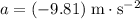`a = (-9.81)\; {\rm m\cdot s^(-2)}`, the time it takes to achieve such velocity change would be:

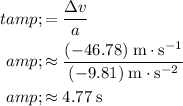`\begin{aligned} t &= (\Delta v)/(a) \\ &\approx \frac{(-46.78)\; {\rm m\cdot s^(-1)}}{(-9.81)\; {\rm m\cdot s^(-2)}} \\ &\approx 4.77\; {\rm s} \end{aligned}`.