Answer: 7.28
Explanation:
This answer is solved by using the Pythagorean Theorem in a clever way. As we know, the Pythagorean Theorem states that:
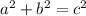
Rewriting this, we find out that it:
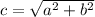
We are using the value C to be the length of AB.
Now that we know how we are solving for c, we can now find values for a and b.
What we want to do, is find sides that will complete a triangle with AB. These sides are measures as:
 (where
(where
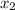 is the x value of coordinate B, and
is the x value of coordinate B, and
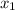 is the x-value of coordinate A) and
is the x-value of coordinate A) and
 (where y is similar to x).
(where y is similar to x).
Now that we have our sides, we can plug them in to the theorem we rewrote before:

We can then begin to solve for AB:
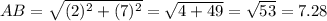
I hope this helps. If you need anything explained more please let me know.