Explanation:
x^2 - 7x -8>0
a=1, b=-7, c=-8
first take notice of the equation, the inequality is > so that means that when you've sketched your graph, the region to be shaded is above the x axis.
then also notice your "a" value, is it positive or negative? in this case it is positive which means you have a minimum curve ( U shape)
okay now that you've derived those information from just the equation, two more final steps before you're able sketch the graph.
1. you must determine the minimum point.
in order to do so, you must find the value of h and k, use the formula for h and k then substitute your a b c values.
recall the formula:
h = b/2a
h = -7/2
h = -3 1/2
-h = 3 1/2
k=
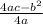
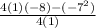
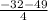
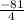
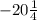
therefore minimum point= (-h,k)
=( 3 1/2, -20 1/4)
2. then you need to simply solve the quadratic equation:
x^2 - 7x -8>0
let x^2 - 7x -8=0
x^2 + x - 8x -8 = 0
factorization
x( x + 1) -8( x + 1) = 0
(x + 1)(x - 8) =0
x+1=0 x-8=0
x= -1 x= 8
now that you've solved the quadratic equation and gotten the two x values, these values show you where the curve cuts the x axis.
okay we have all the information we need now to sketch a graph, draw up your axis at a suitable scale, on x axis 1cm=1 unit, on y axis 2cm=5 units.
insert minimum point and cut the x axis at the two points then draw a smooth free hand curve connecting the points.
remembering the inequality sign, shade the region above the x axis in order to determine solution.
the solution should look like y= {x=ą, x=ß}
since it's above the x axis when y>0 for a minimum curve.
in this case ą and ß is your two x values where ą is the smaller of the two values, -1, and ß is always the larger value, 8.
in conclusion the solution should be y= {x= -1, x=8} when y>0 for a minimum curve.
Note: graph should be done in pencil, include always your title, scale and label your axis unless you're doing a simple sketch of the graph
if you have any questions about the graph or if I did something confusing and you want to know the reasoning behind it, feel free to ask :D hope this helped