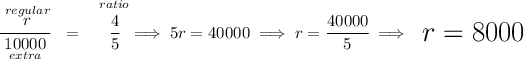well, they found that 5 out of every 9 prefer the extra crunchy version, that means that 4 out of 9 didn't, meaning preferred the regular version, so we can say that the ratio of regular to extra crunchy is 4 : 5.
now, if the company holds to only sell 90000 containers, how many of each, using that ratio above, should they produce?
we can simply divide 90000 by (4 + 5) and then distribute accordingly.
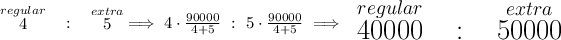
now, if the company decides to only produce 10000 containers of the new crunchy version, how many regular ones are there to produce, keeping in mind that 4 : 5 ratio?