Question

See picture for question

Answer 1

See explanation below

Explanation:

For y = f(x)

if the degree of the denominator is greater than the degree of the numerator, the horizontal asymptote is at y = 0 or f(x) = 0

So for

`\mathsf {y =(x-2)/(x^3)}`,
the horizontal asymptote is at y = 0

To see why this is so, put in a very large number for x and estimate y
Say x = 10^6

`y = (10^6 - 2)/((10^6)^ 3) \approx 0\\\\\text{As } x \rightarrow \infty, y \rightarrow 0`

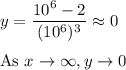
Hence the horizontal asymptote at y = 0