Answer:
See explanation below
Explanation:
For y = f(x)
if the degree of the denominator is greater than the degree of the numerator, the horizontal asymptote is at y = 0 or f(x) = 0
So for
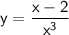 ,
,
the horizontal asymptote is at y = 0
To see why this is so, put in a very large number for x and estimate y
Say x = 10^6
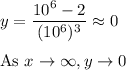
Hence the horizontal asymptote at y = 0