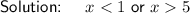Question

X²-6x+5>0 solve to quadratic inequality​

Answer 1

`\large \bf{x < 1} \\ \tt{ or }\\ \large \bf{ x > 5}`

Explanation:

`\bf \longrightarrow {x}^(2) - 6x + 5 > 0`

• Solve for x² - 6x + 5

`\bf \longrightarrow{x}^(2) - 6x + 5 \\ \bf \longrightarrow {x}^(2) - 5x - 1x + 5 \\ \bf \longrightarrow x(x - 5) - 1(x - 5) \\ \bf \longrightarrow(x - 5)(x - 1)`

`\implies(x - 5)(x - 1) > 0`

`\tt{( {x}^(2) = x * x \: \: , \: \: 5 = ( - 1) * ( - 5)}`

`\implies \tt{x < 1 \: or \: x > 5}`

[ 5 and 1 are roots of (x - 5)(x - 1) = 0. So, if you draw a function makes it a little bit clear. ]

Answer 2

`\textsf{Solution: \quad $x < 1$ or $x > 5$}`

`\textsf{Interval notation: \quad $(- \infty, 1) \cup (5, \infty)$}`

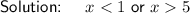
Explanation:

Given inequality:

`x^2-6x+5 > 0`

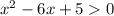
Factor the quadratic to find the x-intercepts

To factor a quadratic in the form
`ax^2+bx+c`, find two numbers that multiply to
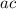`ac` and sum to
`b`:

`\implies ac=a \cdot 5=5`

`\implies b=-6`

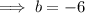
Therefore, the two numbers are: -1 and -5.

Rewrite
`b` as the sum of these two numbers and equal the quadratic to zero:

`\implies x^2-x-5x+5 = 0`

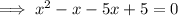
Factor the first two terms and the last two terms separately:

`\implies x(x-1)-5(x-1) = 0`

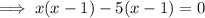
Factor out the common term (x - 1):

`\implies (x-5)(x-1) = 0`

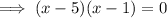
The x-intercepts are when the curve crosses the x-axis (when y=0).

Therefore, the x-intercepts are:

`(x-5)=0 \implies x=5`

`(x-1)=0 \implies x=1`

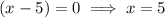
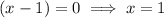
As the leading coefficient of the quadratic is positive, the parabola opens upwards. Therefore, to find the solution of the inequality, find the interval where the curve is positive (above the x-axis).

The curve is above the x-axis when x < 1 or x > 5.

Therefore, the solution to the quadratic inequality is:

`\textsf{Solution: \quad $x < 1$ or $x > 5$}`

`\textsf{Interval notation: \quad $(- \infty, 1) \cup (5, \infty)$}`